Reconnaissance de visage par analyse en composantes principales

1. Introduction

L’apprentissage machine est un sujet d’actualité depuis longtemps. Qu’il s’agisse de découvrir de nouvelles musiques ou de trouver des vêtements que l’on a le goût d’acheter, la technologie est utilisée partout dans la vie de tous les jours à des fins très diverses. Cependant, beaucoup de gens ont peur d’aborder le sujet en raison de sa complexité mathématique. Dans cet article de blogue, je décris brièvement d’une façon de construire un programme de reconnaissance faciale en utilisant une méthode simple de réduction dimensionnelle appelée analyse en composantes principales.

2. Avant de commencer

Qu’est-ce que l’analyse en composantes principales ?

L’analyse en composantes principales est une procédure statistique qui utilise une transformation orthogonale pour convertir un ensemble de variables corrélées en ensembles de variables non corrélées appelés composantes principales.

Les gens qui n’ont pas de connaissances en mathématiques peuvent se sentir découragés en lisant une définition formelle comme celle-ci, mais ce n’est pas aussi compliqué que vous le pensez !

2.1. Transformation orthogonale

Définition mathématique :

Pour comprendre la transformation orthogonale, nous devons comprendre ce qu’est un produit scalaire.

\(x_{1} \cdot x_{2} = |x_{1}||x_{2}|\cos{\theta}\)

Ci-dessus se trouve la définition habituelle du produit scalaire de deux vecteurs euclidiens que les étudiants apprennent au cours de leur carrière académique. Cependant, nous oublions souvent ce qu’elle représente. Il est évident que \(|x_{1}||x_{2}|\) sont les composantes scalaires de ces deux vecteurs, mais que représente \(\cos{\theta}\) ?

Il est bien plus facile de comprendre le terme \(\cos{\theta}\) quand on examine différents cas. Il y a cinq cas à considérer :

Cas 1 où \(x_{1}\) et \(x_{2}\) sont dans la même direction, \(\cos{\theta}\) vaudra 1

Cas 2 où \(x_{1}\) et \(x_{2}\) sont généralement dans la même direction (angle entre 0 et 90), \(\cos{\theta}\) sera une valeur entre 0 et 1.

Cas 3 où \(x_{1}\) et \(x_{2}\) sont perpendiculaires, \(\cos{\theta}\) vaudra 0.

Cas 4 où \(x_{1}\) et \(x_{2}\) sont généralement dans une direction opposée (angle entre 90 et 180), \(\cos{\theta}\) sera une valeur entre 0 et -1.

Cas 5 où \(x_{1}\) et \(x_{2}\) sont complètement en directions opposées, \(\cos{\theta}\) sera -1.

Dans ces cas, \(\cos{\theta}\) représente la relation soit positive, soit négative, entre les deux vecteurs. Ainsi, nous savons maintenant que le produit scalaire de vecteurs est la qualité scalaire de la relation entre ces vecteurs.

Maintenant, nous pouvons commencer à parler de transformation orthogonale. Le vecteur a cette propriété unique qui fait que si vous le multipliez par une matrice, il retournera un autre vecteur.

Prenons \(v = Au\), où \(v\) et \(u\) sont des vecteurs et \(A\) est une matrice.

Essayons de transformer cette propriété en produits scalaires.

\(x_{1} \cdot x_{2} = (Au_{1}) \cdot (Au_{2})\)

Les produits scalaires de vecteurs peuvent s’écrire comme un produit matriciel.

\((Au_{1}) \cdot (Au_{2}) = (Au_{1})^{T}(Au_{2})\)

Utilisation des propriétés de transposition :

\((Au_{1})^{T}(Au_{2}) = u_{1}^{T}A^{T}Au_{2}\)

\( \therefore x_{1} \cdot x_{2} = u_{1}^{T}A^{T}Au_{2} \)

Si \(A\) est une matrice orthogonale, l’équation devient :

\(x_{1} \cdot x_{2} = u_{1}^{T}u_{2} = u_{1} \cdot u_{2}\)

Surprenant ! Les propriétés des produits scalaires sont tranférées dans le nouvel ensemble de vecteurs. C’est ce qu’on appelle la transformation orthogonale. Cela signifie que les nouveaux vecteurs préservent toute la géométrie des vecteurs originaux.

2.2 Analyse en composantes principales

Maintenant, nous pouvons enfin passer à l’analyse en composantes principales, aussi connue sous le nom d’ACP. L’idée derrière les composantes principales est de retracer un ensemble de données sur un axe plus corrélé qui est connu sous le nom de composante principale. Ces axes sont créés par transformation orthogonale.

3. Guide étape par étape

3.1 Prétraitement des données

Tout d’abord, nous devons préparer des images de visage de même dimension \([N \times M]\) qui seront décomposées en un ensemble de vecteurs. Les images avec un même arrière-plan augmenteront la précision puisque l’ACP recherche les variables non corrélées. Ces vecteurs seront stockés sous forme de colonne ou de rangée dans une matrice.

\( \text{Image} = [\ N \times M \ ]\)

\(\text{Image Vectorisée} = [\ ( N \cdot M ) \times 1\ ]\)

\(\text{Matrice Image}= [\ ( N \cdot M) \times NI \ ] = [\ VI_{1}, VI_{2}, VI_{3}, ...\ ]\)

Où NI est le nombre d’images, VI est l’image vectorisée.

Regardons un exemple de code !

Par convention, les vecteurs d’image sont sauvegardés sous forme de colonne dans une matrice, mais dans mon exemple, j’ai sauvegardé sous forme de rangée (oups).

Voici les bibliothèques Python nécessaires :

• Python 3.7
• OpenCV
• Numpy
• TK
• PIL

import os
import numpy as np
import cv2
import tkinter as tk
from tkinter import filedialog
from PIL import Image
#%%
class ImageClass:
    
    # First it is going to grab the folder full of images.
    def __init__(self):
        # Grabbing folder name
        root = tk.Tk()
        root.withdraw()
        self.folder_name = filedialog.askdirectory() 
        
    # Saving vectors in each row instead of column.
    def into_matrix(self, size, rows, array, folder_name):
        
        #Creating an empty array to save vectorized images into.
        i_vectors = []
        
        # Vectorizing all images files
        for files_name in array:
            # reading images and coverting images into gray scaled value.
            img_plt = Image.open(folder_name+"/"+str(files_name)).convert('L')
            img = np.array(img_plt, 'uint8')
            if img is not None:
                if img.shape == 3:
                    img = cv2.cvtColor(
                            img,
                            cv2.COLOR_BGR2GRAY
                            )
                i_vectors.append(np.ravel(img))

        return i_vectors 
            
    def vectorize(self):
        
        # Finding image sizes
        test_file = os.listdir(self.folder_name)[0]
        test_image = Image.open(self.folder_name+"/"+test_file).convert('L')
       	test_image = np.array(test_image, 'uint8')
           
        # Images in the folder
        images = [file_name for file_name in os.listdir(self.folder_name)]
        # Channels will be RGB value.
        height, width = test_image.shape
        size = height * width
    
        # Creating a matrix to save vectorized images
        i_vectors = self.into_matrix(size, len(images), images, self.folder_name)
        return np.matrix(i_vectors), height, width

3.2 Exécution de l’ACP

Puisque nous voulons trouver la caractéristique qui présente le plus de variance, nous devons soustraire la valeur moyenne de la matrice d’image. C’est presque comme déplacer tous les points pour qu’ils soient plus relatifs à l’origine, de sorte que le premier composant principal soit plus qu’une simple représentation de la valeur moyenne de la matrice de l’image.

\(\mu = \frac{1}{NI}\sum_{n=1}^{M} \text{Image Matrix}_{n} \)

\(I_{i} = \text{Image Matrix}_{i} - \mu\)

Maintenant, nous pouvons enfin calculer la variance entre chaque vecteur d’image en calculant la covariance de la matrice.

Selon la configuration de la matrice d’images (en colonnes ou en lignes), vous pouvez réduire votre temps de calcul en effectuant une multiplication matricielle avec le nombre d'images plutôt que le nombre de pixels de l’image.

Si \(I\) a une dimension de \([ NM \times NI ]\) alors :

\(C = \frac{1}{NI}\sum_{n=1}^{M} I \cdot I^{T}\)

Cela réduira le temps de calcul tout en n’affectant pas le processus puisque nous ne sélectionnons qu’un certain nombre de vecteurs propres pour créer des “eigenfaces” (ensembles de vecteurs propres dédiés à la reconnaissance faciale). Les “eigenfaces” peuvent être construites en faisant un produit scalaire avec la matrice d’images et le vecteur propre.

import numpy as np
from numpy import linalg as LA
#%%
# Finding covariance matrix
# B.B^T  instead of B^T.B since it will take too long to calculate and you only need biggest eigenvector
# of B^T.B and it can be done by using eigenvector of B.B^T 
S = (1/(number_of_images-1))*np.dot(B,np.transpose(B))

# Finding eigenvector. I used the NumPy library for this.
w, v = LA.eig(S)

# Calculating eigen_faces
eigen_faces_float = np.dot(np.transpose(B), v)
# So I can translate into unit8 data type
eigen_faces = eigen_faces_float.clip(min=0)
eigen_faces = np.uint8(eigen_faces)

3.3 Reconstitution de visages avec les “eigenfaces”

Utilisons donc ces “eigenfaces” ! Par exemple, je veux recréer mon visage ci-dessous…

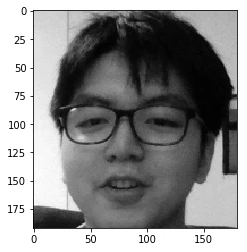
Pour ce faire, nous devons calculer le poids de chaque vecteur propre pour créer le visage souhaité. Les poids peuvent être calculés de cette manière :

for i in range(n_pca):
    weight[i] = np.dot(np.transpose(eigen_faces_norm[i]), testi_vectors_m[:,i])
    magnitude[i] = weight[i]**2
# Threshold value is going to be the magnitude.
TV = np.sqrt(np.sum(magnitude))

« n_pca » est un nombre de composants principaux. J’en ai sélectionné 3 pour cet exemple, mais vous pouvez utiliser plus que 3 “eigenfaces”. Plus il y en a, plus la recréation d’image sera bonne, mais ce sera moins précis lors des tests car plus de caractéristiques qui sont moins nécessaires pour reconstruire le visage sont prises en compte.

La somme des poids sera utilisée comme valeur seuil pour distinguer les différents visages. Ces poids seront utilisés pour reconstruire des visages.

for i in range(3):
    reconstruction[i] = weight[i]*np.transpose(eigen_faces_norm[i])
    reconstruction[i] = reconstruction[i].clip(min=0)
    reconstruction[i] = np.uint8(reconstruction[i])

Nous avons reconstruit le visage ! Mais il est très différent du visage que nous essayons de créer. Oh ! Nous avons oublié d’y ajouter un visage moyen. Nous devons ajouter le visage moyen puisque nous avons soustrait le visage moyen des ensembles de données afin de trouver les différentes caractéristiques.

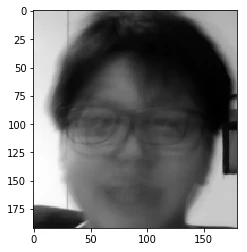
Ci-dessus, le visage moyen.

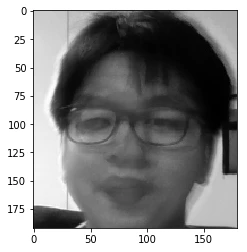
Ci-dessus, le visage reconstruit ; il est assez similaire à celui que nous recherchons.

3.4 Test

Nous y sommes presque. Maintenant, nous devons créer un ensemble d’entraînement dans lequel nous vérifierons si nous pouvons détecter différents visages.

# Selecting the folder full of probe images.
probe_images = vc.ImageClass()
probe_images_m, prh, prw = probe_images.vectorize()
probe_images_m = probe_images_m - mean
probe_weights = np.zeros((n_pca,1))
#%%
for i in range(len(probe_images_m)):
    for c in range(n_pca):
        probe_weights[c] = np.dot(np.transpose(eigen_faces_norm[c]), np.transpose(probe_images_m[i]))
    weight_c = np.zeros((n_pca,1))
    for z in range(n_pca):
        weight_c[z] = (weight[z] - probe_weights[z])**2
    weight_c_min = np.sqrt(np.sum(weight_c))
    if weight_c_min <= np.sqrt(np.sum(magnitude)):
        print("yes")
    else:
        print("no")

Les poids des tests sont calculés de la même manière que les autres. Il suffit de comparer la magnitude des ensembles d’entraînement et celle de chaque image dans les ensembles de tests.