Face recognition by principal component analysis

In this article, June from Spiria Toronto explains the basics of facial recognition using the principal component analysis method.
1. Introduction
Machine learning has been a hot topic for a while. From discovering new music to finding clothes we might want to purchase, it is used in many aspects of our daily lives for many different purposes. However, many people are afraid to approach it due to its mathematical complexity. In this blog, I will briefly talk about one way to build facial recognition programs using a simple dimensionality-reduction method called principal component analysis.
2. Before We Start
What is principal component analysis?
Principal component analysis is a statistical procedure that uses an orthogonal transformation to convert a set of correlated variables into sets of uncorrelated variables called principal components.
People without a mathematical background can get discouraged from reading formal definitions like this, but it is not as complicated as you think it is!
2.1. Orthogonal Transformation
Mathematical definition:
To understand orthogonal transformation, we first need to understand what inner product space is, also known as dot product.
\(x_{1} \cdot x_{2} = |x_{1}||x_{2}|\cos{\theta}\)
This is the usual definition of a dot product that students learn during their academic career. However, we often forget what it stands for. Let’s go through each term and understand what it means. It is obvious that \(|x_{1}||x_{2}|\) represents scalar components of these two vectors, but what does \(\cos{\theta}\) represent?
It is much easier to understand the term \(\cos{\theta}\) when we look at different situations. There are five cases to consider:
Case 1 when \(x_{1}\) and \(x_{2}\) lie in the same direction, \(\cos{\theta}\) is 1
Case 2 when \(x_{1}\) and \(x_{2}\) lie generally in the same direction (angled between 0 and 90), \(\cos{\theta}\) has a value between 0 and 1.
Case 3 when \(x_{1}\) and \(x_{2}\) lie perpendicular to one another, \(\cos{\theta}\) is 0.
Case 4 when \(x_{1}\) and \(x_{2}\) generally lie in the opposite direction (angled between 90 and 180), \(\cos{\theta}\) has a value between 0 and -1.
Case 5 when \(x_{1}\) and \(x_{2}\) lie in the complete opposite direction, \(\cos{\theta}\) has a value of -1.
Given these cases, \(\cos{\theta}\) represents a relationship between pairs of vectors, i.e. whether one vector affects the other negatively or positively. Thus, we now know that the dot product of vectors are scalar qualities of relationships between vectors.
Now, we can start talking about orthogonal transformation. Vectors have the unique property where if you multiply a vector by a matrix, it will return another vector.
Take \(v = Au\), where \(v\), and \(u\) are vectors and \(A\) is a matrix.
Let’s try substituting this property into dot products.
\(x_{1} \cdot x_{2} = (Au_{1}) \cdot (Au_{2})\)
Dot products of vectors can be written as a matrix product:
\((Au_{1}) \cdot (Au_{2}) = (Au_{1})^{T}(Au_{2})\)
Using the properties of transposition,
\((Au_{1})^{T}(Au_{2}) = u_{1}^{T}A^{T}Au_{2}\)
\( \therefore x_{1} \cdot x_{2} = u_{1}^{T}A^{T}Au_{2} \)
If \(A\) is an orthogonal matrix, then the equation becomes:
\(x_{1} \cdot x_{2} = u_{1}^{T}u_{2} = u_{1} \cdot u_{2}\)
Surprise! The dot products properties have been translated into a new set of vectors. This is called orthogonal transformation. This means that the new vectors preserve all the geometry of the original vectors.
2.2 Principle Component Analysis
Now, we can finally get into principal component analysis (also known as PCA). The idea is to re-plot a set of data to more correlated axes, which is known as principal component. These axes are created by using orthogonal transformation.
3. Step-by-Step Guide
3.1 Data Preprocessing
First, we need to prepare facial images with the same dimensions \([N \times M]\), which will be unraveled into a set of vectors. Images with the same background will have more accuracy since PCA looks for uncorrelated variables. These vectors will be stored as either a column or a row in a matrix.
\( \text{Image} = [\ N \times M \ ]\)
\(\text{Vectorized Image} = [\ ( N \cdot M ) \times 1\ ]\)
\(\text{Image Matrix}= [\ ( N \cdot M) \times NI \ ] = [\ VI_{1}, VI_{2}, VI_{3}, ...\ ]\)
where NI is the number of image, VI is the vectorized image.
Let’s look at a code example!
Conventionally, image vectors are saved as columns in a matrix but in my example, I saved them as a row (oops).
These are the dependent Python libraries:
- Python 3.7
- OpenCV
- Numpy
- TK
- PIL
import os
import numpy as np
import cv2
import tkinter as tk
from tkinter import filedialog
from PIL import Image
#%%
class ImageClass:
# First it is going to grab the folder full of images.
def __init__(self):
# Grabbing folder name
root = tk.Tk()
root.withdraw()
self.folder_name = filedialog.askdirectory()
# Saving vectors in each row instead of column.
def into_matrix(self, size, rows, array, folder_name):
#Creating an empty array to save vectorized images into.
i_vectors = []
# Vectorizing all images files
for files_name in array:
# reading images and coverting images into gray scaled value.
img_plt = Image.open(folder_name+"/"+str(files_name)).convert('L')
img = np.array(img_plt, 'uint8')
if img is not None:
if img.shape == 3:
img = cv2.cvtColor(
img,
cv2.COLOR_BGR2GRAY
)
i_vectors.append(np.ravel(img))
return i_vectors
def vectorize(self):
# Finding image sizes
test_file = os.listdir(self.folder_name)[0]
test_image = Image.open(self.folder_name+"/"+test_file).convert('L')
test_image = np.array(test_image, 'uint8')
# Images in the folder
images = [file_name for file_name in os.listdir(self.folder_name)]
# Channels will be RGB value.
height, width = test_image.shape
size = height * width
# Creating a matrix to save vectorized images
i_vectors = self.into_matrix(size, len(images), images, self.folder_name)
return np.matrix(i_vectors), height, width
3.2 Performing PCA
Since we want to find the feature with the most variance, we need to subtract the mean value from the image matrix. It is almost like moving all the points to be more relative to the origin so that the first principal component will be more than just a mere representation of the mean value of the image matrix.
\(\mu = \frac{1}{NI}\sum_{n=1}^{M} \text{Image Matrix}_{n} \)
\(I_{i} = \text{Image Matrix}_{i} - \mu\)
Now, we can finally figure out the variance between each image vector by calculating the covariance of the matrix.
Depending on how the image matrix is set up (in columns or in rows), you can reduce your calculation time by performing a matrix multiplication with respect to the number of images instead of the number of pixels within the image.
If \(I\) has a dimension of \([ NM \times NI ]\) then,
\(C = \frac{1}{NI}\sum_{n=1}^{M} I \cdot I^{T}\)
This will reduce the calculation time without affecting the process since we are only picking a certain number of eigenvectors to create eigenfaces. Eigenfaces can be constructed by performing dot multiplications with the image matrix and the eigenvector.
import numpy as np
from numpy import linalg as LA
#%%
# Finding covariance matrix
# B.B^T instead of B^T.B since it will take too long to calculate and you only need biggest eigenvector
# of B^T.B and it can be done by using eigenvector of B.B^T
S = (1/(number_of_images-1))*np.dot(B,np.transpose(B))
# Finding eigenvector. I used the NumPy library for this.
w, v = LA.eig(S)
# Calculating eigen_faces
eigen_faces_float = np.dot(np.transpose(B), v)
# So I can translate into unit8 data type
eigen_faces = eigen_faces_float.clip(min=0)
eigen_faces = np.uint8(eigen_faces)
3.3 Reconstructing Faces Using Eigenfaces
Let’s use these eigenfaces for something fun! For example, I want to recreate my face below…
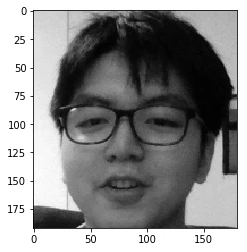
To do this, we need to calculate weights for each eigenvector to create the face we want. Weights can be calculated in this way:
for i in range(n_pca):
weight[i] = np.dot(np.transpose(eigen_faces_norm[i]), testi_vectors_m[:,i])
magnitude[i] = weight[i]**2
# Threshold value is going to be the magnitude.
TV = np.sqrt(np.sum(magnitude))
““n_pca” is the number of principal components. I selected three for this example, but you can use more than three eigenfaces. The more eigenfaces the better the recreated image, but the less accurate the testing. This is because the analysis will account for more features than necessary to reconstruct the face.
The sum of the weights will be used as a threshold value to distinguish different faces. These weights will be used to reconstruct the faces.
for i in range(3):
reconstruction[i] = weight[i]*np.transpose(eigen_faces_norm[i])
reconstruction[i] = reconstruction[i].clip(min=0)
reconstruction[i] = np.uint8(reconstruction[i])

We reconstructed the face! But why is it so different from the face that we were trying to create? Oh! We forgot to add the mean face to it. We need to add the mean face since we subtracted it from the data sets to find the different features.
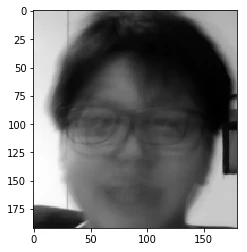
Above is the mean face.
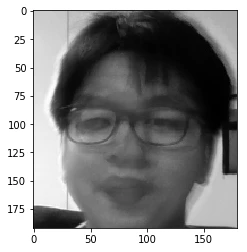
Above is the reconstructed face; it is pretty similar to the face that we were looking for.
3.4 Testing
We’re almost done. Now, we must create a training set to check whether we can detect different faces.
# Selecting the folder full of probe images.
probe_images = vc.ImageClass()
probe_images_m, prh, prw = probe_images.vectorize()
probe_images_m = probe_images_m - mean
probe_weights = np.zeros((n_pca,1))
#%%
for i in range(len(probe_images_m)):
for c in range(n_pca):
probe_weights[c] = np.dot(np.transpose(eigen_faces_norm[c]), np.transpose(probe_images_m[i]))
weight_c = np.zeros((n_pca,1))
for z in range(n_pca):
weight_c[z] = (weight[z] - probe_weights[z])**2
weight_c_min = np.sqrt(np.sum(weight_c))
if weight_c_min <= np.sqrt(np.sum(magnitude)):
print("yes")
else:
print("no")
Probe weights are calculated in the same way that the image weights were calculated. We just need to compare the magnitude of the training sets and the magnitude for each image in the test sets.
