Concepts de programmation multithreads

Introduction
Depuis déjà bon nombre d’années, la fréquence des microprocesseurs (CPU), jusque-là facteur déterminant de la performance des ordinateurs, a cessé de croître. Plusieurs raisons expliquent cela [1] :
- Difficulté à dissiper la chaleur produite par le microprocesseur.
- Besoins en alimentation électrique grandissants.
- Fuites de courant liées à la miniaturisation des transistors.
En réponse aux besoins toujours croissants des applications modernes, une des solutions proposées par les manufacturiers est d’augmenter le nombre de cœurs par microprocesseur. Concrètement, cela veut dire que dans notre ordinateur, au lieu d’avoir un seul cœur exécutant son travail toujours plus vite, nous avons maintenant plusieurs (2, 4, 8…) cœurs de vitesse moyenne, mais pouvant travailler en parallèle.
Génial ! Cela veut dire qu’avec 8 cœurs, mes tâches s’effectueront toutes 8 fois plus vite qu’avant ?
Euh… Ce n’est pas si simple. Un sage m’a déjà dit : si 9 femmes tentent d’accoucher d’un bébé, est-ce qu’elles pourront le faire en 1 mois ?
Certaines tâches ne sont tout simplement pas parallélisables : elles doivent être sérialisées. C’est-à-dire qu’elles doivent nécessairement s’accomplir dans un ordre précis, une après l’autre.
Nous verrons dans cet article comment bien tirer parti de la programmation multithreads.
Concepts de base
Deux principales techniques permettent d’optimiser le gain en performance dont nous pouvons bénéficier à l’aide de la programmation multithreads : le parallélisme de données (Single Instruction, Multiple Data – SIMD) et le parallélisme de tâches (Multiple Instruction, Multiple Data – MIMD).
Parallélisme de données (SIMD)
Le parallélisme de données consiste en la distribution d’un ensemble de données à calculer de la même façon en plusieurs groupes pouvant être calculés en même temps sur plusieurs cœurs.
Voici quelques exemples qui permettent de mieux comprendre de quoi il s’agit.
Exemple 1 :
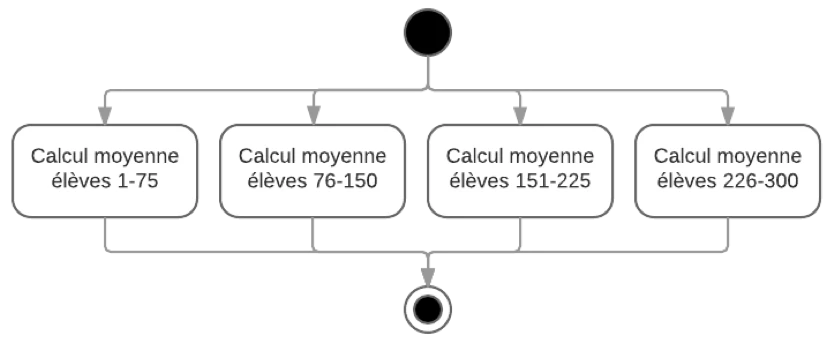
Si on doit calculer la moyenne académique individuelle de 300 élèves d’une école, et que l’on dispose d’un microprocesseur à 4 cœurs, on peut diviser le groupe en 4 groupes de 75 élèves, et calculer la moyenne des élèves de chacun de ces 4 groupes sur un cœur séparé en même temps. On peut facilement imaginer être capable d’effectuer le calcul presque [2] 4 fois plus vite qu’avec un seul cœur.
Simple ? Parfait. Compliquons les choses un peu.
Exemple 2 :
En prenant toujours le même groupe de 300 élèves, nous devons maintenant calculer le rang centile de chaque élève ; c’est-à-dire, le pourcentage d’élèves du groupe dont la moyenne se situe en dessous de chaque élève. La formule mathématique pour faire le calcul est la suivante [3] :
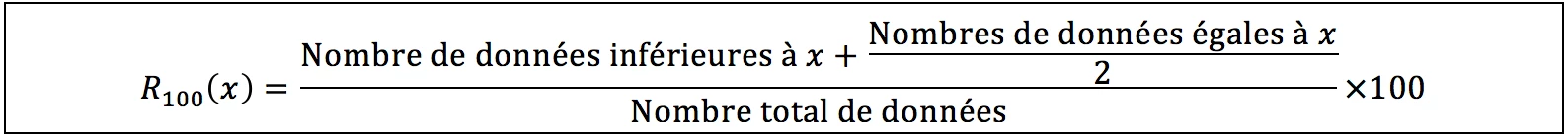
Le problème devient instantanément plus compliqué du fait que nous avons maintenant besoin des données de chaque élève afin de calculer le rang centile des autres.
Dans le premier exemple, la séparation des tâches s’avère très intuitive : chaque calcul de moyenne ne nécessite que les résultats scolaires d’un seul élève.
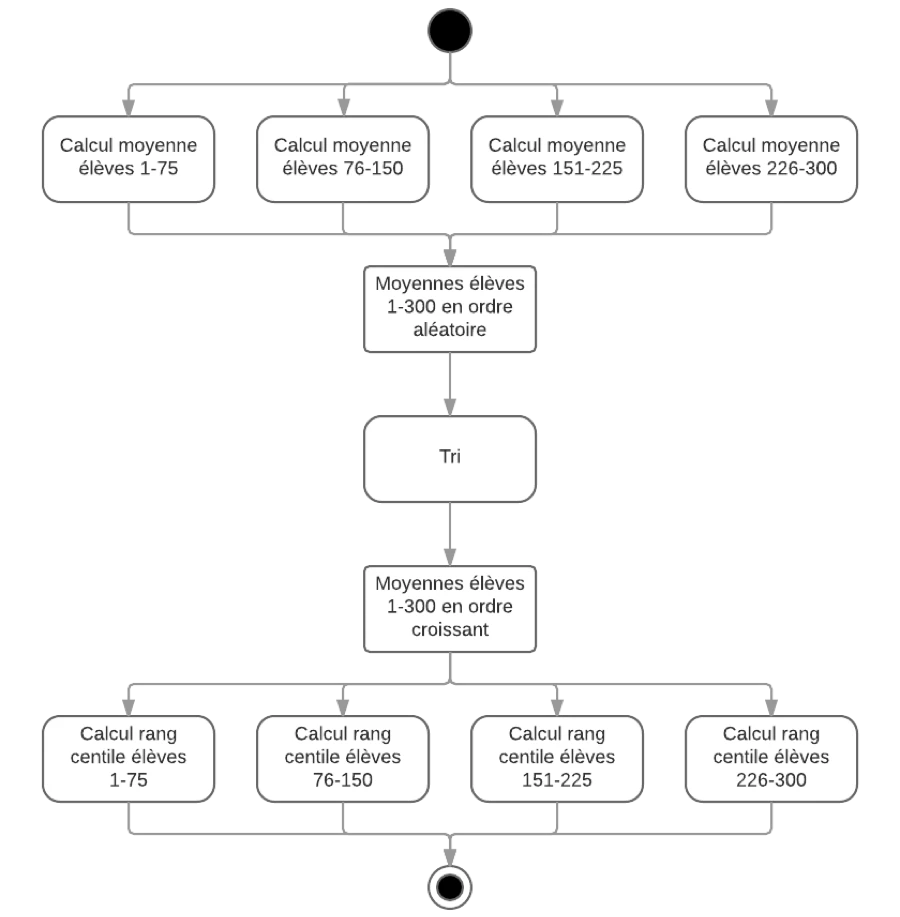
Dans le second exemple, il est moins intuitif de séparer les tâches. Il y a probablement des algorithmes permettant une parallélisation plus efficace (je ne suis pas mathématicien), mais une des méthodes simples d’effectuer ce calcul serait de :
- Calculer la moyenne de chaque élève du groupe en parallèle (comme pour l’exemple 1).
- Ordonner les moyennes de chaque élève en utilisant un algorithme de tri.
- Distribuer le calcul du rang centile de chaque élève en créant 4 groupes de 75 élèves, et en rendant disponible en lecture à chaque groupe :
- la moyenne de chaque élève du sous-groupe de 75 élèves ;
- la liste complète ordonnée des moyennes de tous les élèves du groupe de 300.
Comme vous pouvez le constater, même si plusieurs étapes du calcul peuvent s’effectuer de manière parallèle (au moins les étapes 1 et 3), les étapes, elles, doivent être calculées dans un ordre précis, une après l’autre. Même si le calcul des moyennes du groupe 1 est terminé avant les autres, il est impossible de calculer le rang centile de ce dernier avant que tous les autres groupes aient aussi terminé leurs calculs. Si on tentait de le faire (en utilisant seulement les résultats partiels du groupe 1), nous aurions un problème de concurrence (race condition) où les résultats du calcul pourraient varier d’une exécution à l’autre, dépendamment l’ordre dans lequel les groupes de l’étape 1 termineraient leur travail.
Cet ordre nécessaire est ce qu’on appelle la composante sérielle de l’algorithme. Cette composante est ce qui viendra limiter le gain en performance lié à la parallélisation de notre algorithme.
Parallélisme de tâches
Le parallélisme de tâches consiste en l’exécution de tâches disparates, n’ayant peu ou pas de lien commun, sur des cœurs différents en même temps.
Par exemple, si vous êtes en train d’écouter de la musique sur votre ordinateur en même temps que vous naviguez sur le web, et que votre ordinateur possède plusieurs cœurs, il y a de fortes chances que ces deux tâches soient exécutées en même temps sur deux cœurs différents.
Cela est très pratique, puisqu’en théorie, il est possible d’augmenter d’autant de fois que le nombre de CPUs la quantité de travail que votre ordinateur peut faire en même temps. Cependant, pour être capable d’effectuer l’ordonnancement de toutes ces tâches, le système d’exploitation doit fournir un effort non-négligeable pour constamment (ré) évaluer la priorité de chaque tâche, gérer le temps à allouer pour chacune d’elle, gérer les interruptions qui peuvent survenir au fil de l’exécution, gérer l’accès aux ressources limitées du système entre les différents processus, etc. Cet effort vient lui aussi limiter l’augmentation en performance atteinte par ce type de parallélisme.
Il est aussi possible d’effectuer du parallélisme par tâches au sein d’une même application. Par exemple, une application peut dans un fil d’exécution (thread) gérer le dessin et les interactions de son interface usager, et dans un autre sauvegarder le document en cours. La plupart du temps, ces deux tâches sont complètement indépendantes. Dans certaines conditions, par contre, un lien entre les deux actions nécessitera l’utilisation d’un mécanisme de synchronisation pour éviter les problèmes de concurrence. Dans le cas précis de cet exemple, il faudrait éviter de permettre à l’usager de fermer l’application avant qu’une sauvegarde soit terminée, pour éviter que l’usager ne perde ses données.
Les techniques pour synchroniser différents threads seront détaillées dans un article futur.
Limites de la programmation multithreads
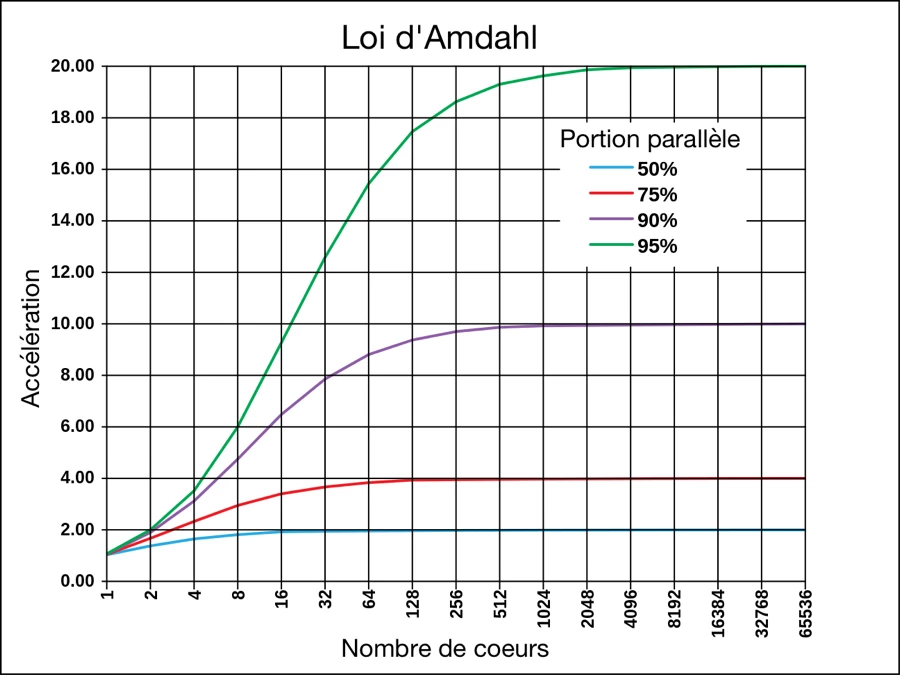
Comme nous avons pu le voir, bien qu’on soit tentés de croire que le fait de multiplier les cœurs disponibles pour effectuer un travail accélérerait l’exécution de ce travail d’un facteur égal au nombre de cœurs utilisés pour l’accomplir, la réalité en est autrement.
Le scientifique Gene Amdahl a énoncé la Loi d’Amdahl, qui décrit la limite théorique en accélération en latence du temps d’exécution d’une tâche comme suit :
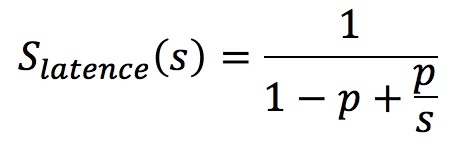
où
- S latence : accélération théorique de l’algorithme.
- s : accélération théorique de la partie parallélisable de l’algorithme (simplification : nombre de cœurs).
- p : pourcentage du temps d’exécution de la partie parallélisable de la tâche.
Donc, si nous avons un algorithme dont 70 % de l’exécution est parallélisable, le gain théorique maximal que l’on peut atteindre en parallélisant cette partie sur 8 cœurs serait comme suit :
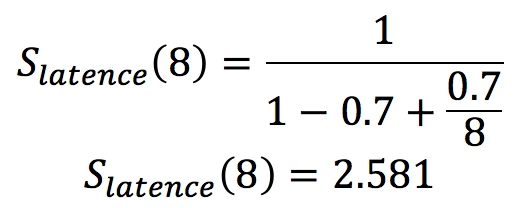
Même si nous avons 8 cœurs, notre tâche ne se terminera qu’au maximum 2 581 plus rapidement que si on n’en avait qu’un seul. Il est donc primordial de chercher, à l’aide d’optimisations ou de réorganisation de l’algorithme, à minimiser la portion sérielle (non-parallélisable) de celui-ci afin de maximiser l’accélération que l’on peut apporter à notre algorithme à l’aide du parallélisme.
Une autre information importante qui nous est donnée par la loi d’Amdahl est que l’accélération atteinte en augmentant le nombre de cœurs utilisés dans le travail a une limite. À un certain moment, l’ajout de cœurs supplémentaires pour effectuer la tâche ne réduit plus le temps requis pour faire le travail.
Défis
Cet article se voulant une description des concepts de base de la programmation multithreads, nous n’avons pu faire qu’un survol. Dans de prochains articles, nous détaillerons les principaux défis de la programmation multithreads, ainsi qu’un aperçu de quelques outils qui peuvent aider un programmeur à créer et maintenir des applications multithreads.
[1] Sutter, H. The Free Lunch Is Over—A Fundamental Turn Toward Concurrency in Software, GotW.ca, http://www.gotw.ca/publications/concurrency-ddj.htm (consulté le 1er septembre 2016).
[2] Nous verrons d’où vient le “presque” un peu plus loin.
[3] Allô Prof. Mathématique – Le rang centile, alloprof.qc.ca, http://www.alloprof.qc.ca/BV/pages/m1371.aspx (consulté le 1er septembre 2016).
[4] Contributeurs de Wikipedia. Amdahl’s law, Wikipedia, https://en.wikipedia.org/w/index.php?title=Amdahl%27s_law& oldid=732105521 (consulté le 1er septembre 2016).