How to Keep your Train from going off the Rails

Thirty years ago, I received a beautiful electric train set.It came with three different kinds of rails:

Thirty years ago, I received a beautiful electric train set.
It came with three different kinds of rails:

- straight rails,
- curved rails,
- and… curved rails… what ? Again?!
Years later, this third type of rail still puzzled me. The second kind of rail was definitely arc-shaped, but the third had a funny curve to it.
One thing was sure: when I would build an oval run, if I didn’t put the right rails in the right place, my train was guaranteed to derail at high speed.

All aboard the clothoid!
Enough with the teaser. The mystery curve was called a clothoid, or Euler spiral, or just spiral among friends.
A clothoid is the result of a specific mathematical formula that defines a curve whose curvature changes linearly with its curve length.
By definition, the radius of a curve is:
- the radius of a circle (in our case, the second type of rail),
- infinity for straight rails (i.e. the same rails with an infinite radius).
Following the sequence below (called “S-C-S” for Spiral-Curve-Spiral):
- rail-straight, R = +∞,
- rail-spiral, R : +∞ → 60 cm,
- rail-curve, R = 60 cm,
- rail-spiral, R : 60 cm → +∞,
- rail-straight, R = +∞,
the train trip becomes much smoother, without the risk of derailments!
To better understand the effect, let’s take another example from railroads:
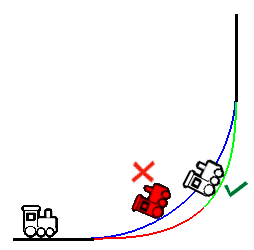
The blue curve is exclusively made up of arcs from a circle with a 60-cm radius, while the green and red curve is made up of two different spirals.
If we now represent the curve (1/R) along the road, this is what we get:
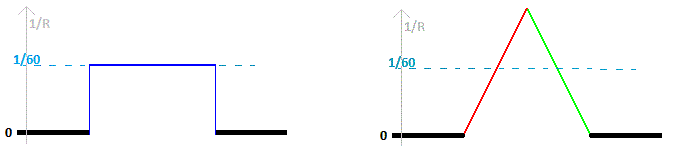
The second itinerary is longer, but free of curvature breaks. This type of curve has many applications in civil engineering: for roads, bridges, railroads, mechanics.
Remember this next time you take a highway exit safely at 100 km/h!
Why are clothoids also called spirals?
Looking at the math behind the curve, if you draw such a curve on an infinite trajectory, this is what you get:
Two symmetrical spirals.
In the rest of this article, we’ll use the following symbols:
| R | Radius of curvature at any given point in a trajectory. Given that R = +∞ at the beginning of the trajectory. |
|---|---|
| φ | Angle between the tangent to the trajectory at any given point and the axis of the abscissa. φ = 0 at the beginning. |
| L | Distance travelled along the curve at any given point. L = 0 at the beginning. |
| A | Constant describing the change in the radius of the curve along the trajectory, by definition: 1/R = L x 1/A2, i.e. A2 = RL |
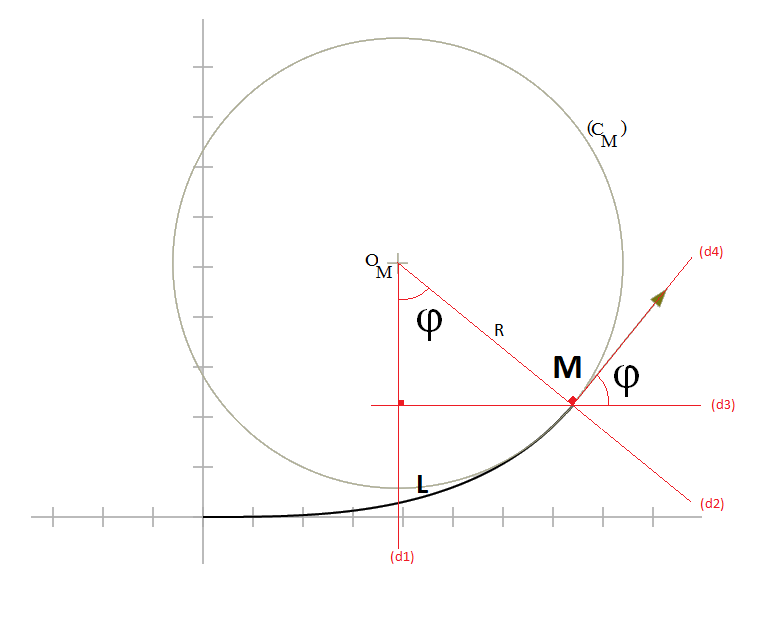
Note that in this figure, the two φ angles are identical:
- φ = internal angle between (d1) and (d2).
- (d3) is perpendicular to (d1) by construction.
- (d4) is perpendicular to (d2), since it is the tangent of circle CM at point M.
- Therefore the angle between (d3) and (d4) is also φ.
Let’s draw a clothoid!
Now let’s draw our own spiral.
If we imagine the trajectory of point M(x,y) along the following itinerary:
- from the curved abscissa L1 (=0),
- to the curved abscissa L2 (=L length of trajectory),
we get:
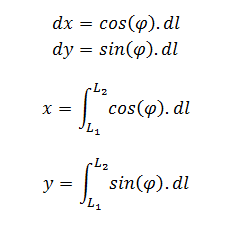
Note that φ is indeed a function of l:
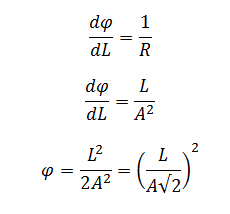
So, given:
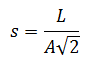
we get:
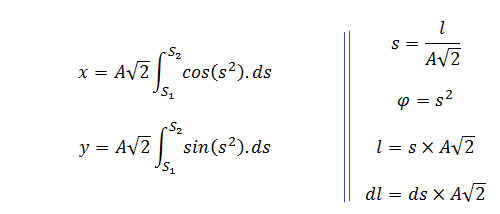
which gives us the following JavaScript code:
function drawSpiral(A, L1, L2)
{
var a = A*Math.sqrt(2);
var S1 = L1/a;
var S2 = L2/a;
var s=S1;
var ds = Math.abs(S2-S1)/10000;
var M = new Point(0,0);
while (s
Result
- Length :
- StartRadius :
- isCCW:
- isEntry:
- ClothoideConstant:
