Basic Concepts in Multithreaded Programming

Introduction

A number of years ago now, microprocessor (CPU) frequency, which until then had been an indicator of a computer’s performance potential, levelled off. There are several reasons for this [1]:

• Difficulty in dissipating the heat produced by the microprocessor.
• Growing energy requirements.
• Current leaks due to the miniaturisation of transistors.

To meet the ever-growing needs of modern applications, manufacturers have experimented with the idea of increasing the number of cores per microprocessor. This would mean that instead of having one single, faster core, your computer would have 2, 4, 8, or more cores working together at a slower frequency, but in parallel.

Great! you think; this means that with 8 cores, my computer will be 8 times faster, right? Um… it’s not that simple: if 9 women worked together to gestate one baby, would it take just one month? Some tasks just can’t be distributed over several cores and run in parallel: they must be done sequentially, or in series.

This article will explain how to take full advantage of multithreaded programming.

Basic Concepts

There are two basic ways to optimize performance through multithreaded programming: data parallelism (Single Instruction, Multiple Data – SIMD) and task parallelism (Multiple Instruction, Multiple Data – MIMD).

Data parallelism (SIMD)

Data parallelism consists in distributing a set of data over several cores in order for them to do identical calculations simultaneously, each on their own subset of data.

Let’s take a couple of concrete examples.

Example 1:

Say you have to calculate the individual academic average of 300 students. On a four-core processor, the students can be divided up into four 4 groups of 75, each core calculating 75 students’ average simultaneously. In this case, the calculation would be done almost four times faster [2] than on a single core.

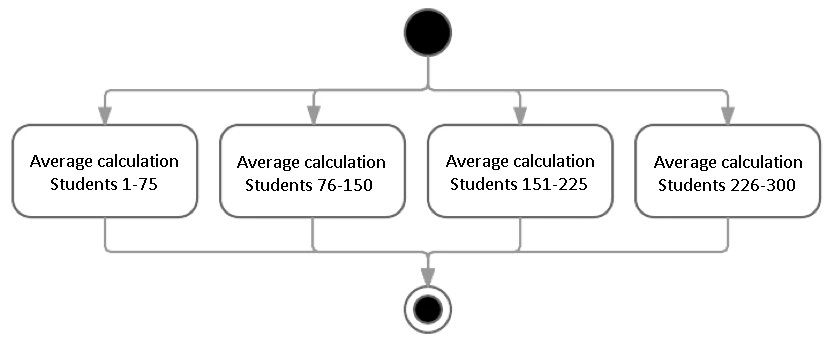
Sounds simple? Excellent. Now let’s get complicated.

Example 2:

Say you now want to calculate the percentile ranking of each of these 300 students; in other words, the percentage of scores that are equal to or lower than each student’s score. Here is the mathematical formula [3]:

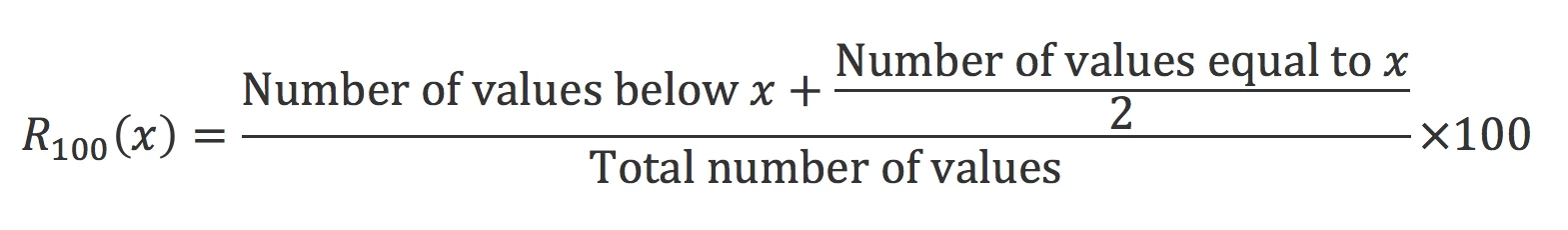
The problem is trickier, since we now need to know the values for all students in order to calculate the percentile ranking of each student.

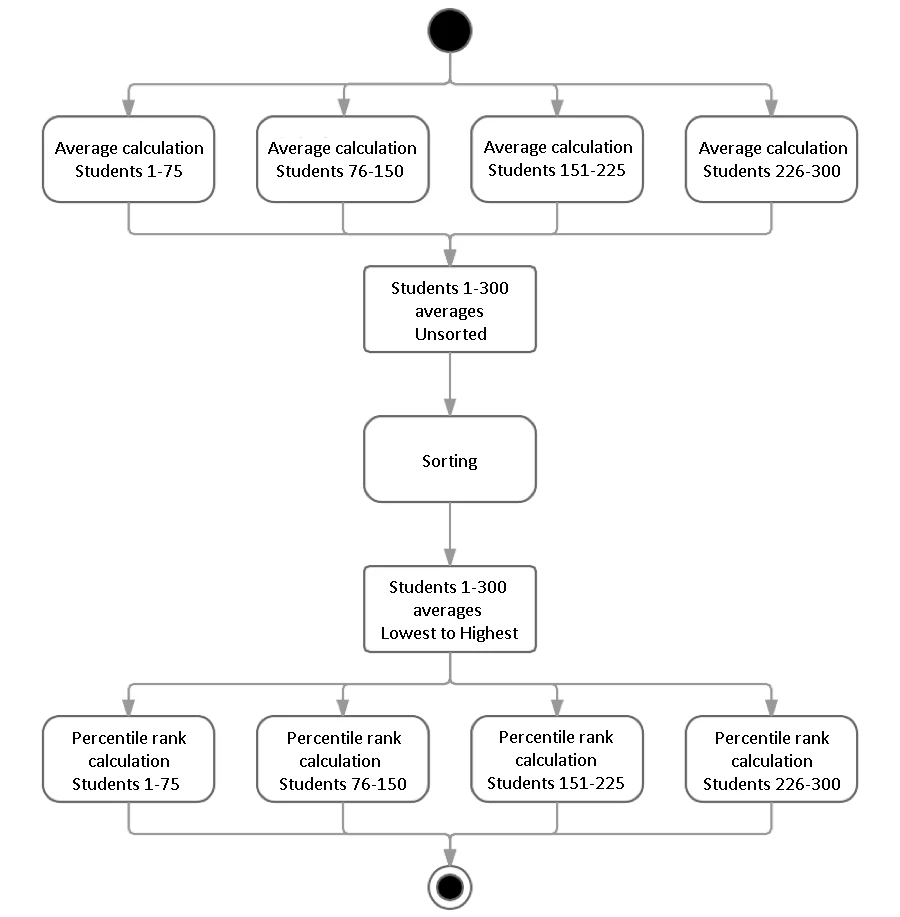
In example 1, task separation is intuitive, since each average calculation only requires the grades of one student.

In example 2, splitting up the tasks is less intuitive. There are probably algorithms to optimize parallelism, but since I am no mathematician, here is a simple way of doing it:

1. Calculate the average of each student in four parallel groups (as per example 1).
2. Rank the averages using a sorting algorithm.
3. Distribute each student’s percentile ranking calculation over four groups of 75, making the following available in read-only format to every other group:
   1. the average of each student in each sub-group of 75;
   2. the complete, ranked list of averages for all 300 students.

As you can see, while several steps of the calculation can be performed in parallel (i.e., at least steps 1 and 3), each one of these steps must be performed sequentially, in a specific order. This means that even though one core may have finished calculating averages before the others, it cannot go on to the next step and calculate percentile rankings until all cores are finished. If we tried to do so using just the result of one group, we would have a concurrency problem (“race condition”) where the results of the calculations would vary from one execution to the next, depending on the order in which the cores finished their step 1 calculations.

This specific order of execution is what is called the serial component of the algorithm, and it will hamper the performance gains of parallelism.

Task Parallelism

Task parallelism consists in distributing the execution of unrelated tasks over several cores in order for them to be performed simultaneously.

For example, if you’re streaming music through your computer while surfing the Web, and your computer is equipped with more than one core, chances are that these two tasks are being performed by two different cores.

This can be very useful since, in theory, your computer can simultaneously perform as many tasks as it has CPUs. This said, in order to manage all these tasks, the operating system has to put in quite a bit of effort to continuously re-evaluate the priority of each task, manage the time allocated to each one, manage any interruptions in their execution, manage competing processes’ access to the system’s limited resources, etc.… This operating system effort also limits the performance gains of parallelism.

It is also possible to distribute tasks within one single application. For example, within an application, one thread can manage graphics and user interface interactions, while another can save the document being worked on. Most of the time, these two tasks are completely independent one from the other. However, in certain circumstances, these two actions are linked; it then becomes necessary to synchronize them, in order to avoid a race condition. In this instance, you would have to make it impossible for the user to close the application before saving, in order to avoid losing any data

Techniques to achieve proper thread synchronization will be detailed in an upcoming article.

Limits of Multithreaded Programming

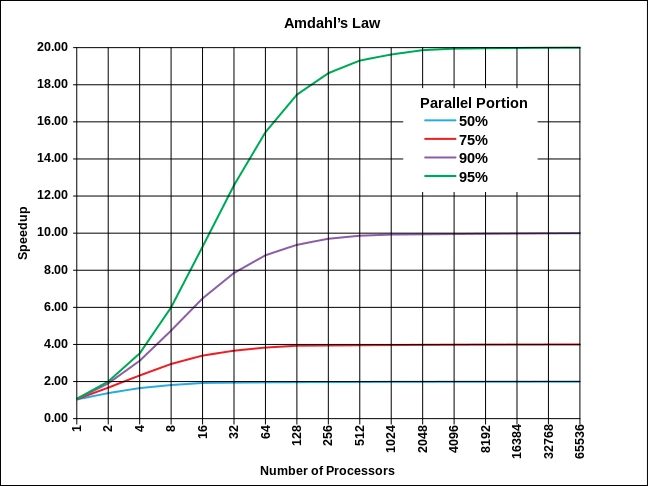
As we have seen, though it would be nice to say that increasing the number of cores speeds up the work by a factor equivalent to the number of cores used to accomplish it, things are quite different in reality.

Donc, si nous avons un algorithme dont 70 % de l’exécution est parallélisable, le gain théorique maximal que l’on peut atteindre en parallélisant cette partie sur 8 cœurs serait comme suit :

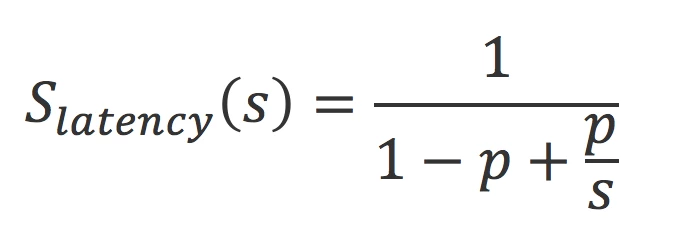
where

• S _latency: theoretical speedup of the algorithm.
• s: theoretical speedup of the part of the algorithm that can be executed in parallel (i.e. number of cores).
• p: percentage of the execution time of the algorithm representing work executed in parallel.

So, say you have an algorithm, 70% of which can be executed in parallel. The maximum theoretical gain that can be achieved by distributing it over 8 cores is as follows:

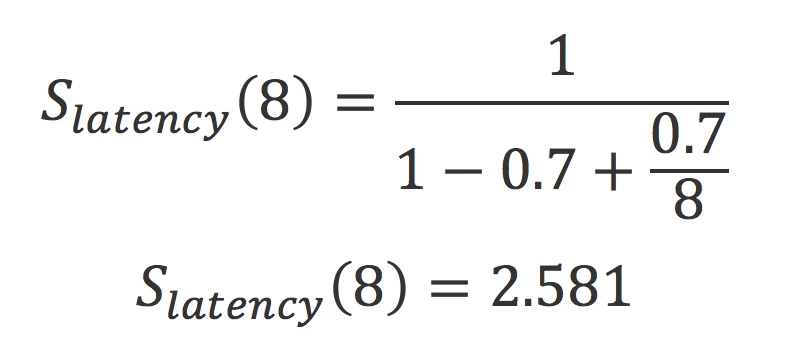
Even though there are 8 cores, the task can only be completed 2.581 times faster than with a single core. Hence the importance of optimizing and reorganizing the algorithm in order to minimize the portion of the algorithm that can’t be distributed.

Another important piece of information provided by Amdahl’s Law is that the acceleration achieved by increasing the number of cores used in a task has limits. There comes a time when adding cores no longer speeds up the process.

 [4]

Challenges

Since this article seeks only to provide a description of basic concepts of multithreaded programming, we’ve only provided an overview. In future articles, we’ll go over the main challenges of multithreaded programming and present tools to help programmers create and maintain multithreaded applications.

 [1] Sutter, H. The Free Lunch Is Over—A Fundamental Turn Toward Concurrency in Software, GotW.ca, http://www.gotw.ca/publications/concurrency-ddj.htm (accessed on September 1^st, 2016).

 [2] We’ll explain the “almost” further down.

 [3]Allô Prof. Mathématique – Le rang centile, alloprof.qc.ca, http://www.alloprof.qc.ca/BV/pages/m1371.aspx (accessed on September 1^st, 2016).

 [4] Contributeurs de Wikipedia. Amdahl’s law, Wikipedia, https://en.wikipedia.org/w/index.php?title=Amdahl%27s_law& oldid=732105521 (accessed on September 1^st, 2016).