Comment éviter de faire dérailler son train électrique ?

Il y a 30 ans, j’ai reçu un superbe train électrique.Il y avait à l’époque 3 modèles de rails différents dans la boîte :

Il y a 30 ans, j’ai reçu un superbe train électrique.
Il y avait à l’époque 3 modèles de rails différents dans la boîte :

- des rails pour aller tout droit,
- des rails pour tourner,
- et… des rails pour tourner… Quoi ? Encore ?!
Même des années plus tard, un certain mystère entourait toujours ces rails de troisième type.
En effet, si le second type était manifestement un “bout” de cercle, le troisième était une sorte de courbe étrange…
Une chose était sûre : si l’on cherchait à réaliser un trajet de forme ovale et que l’on ne mettait pas les bons rails aux bons endroits, le train déraillait inévitablement lorsqu’il allait trop vite !

En route vers les clothoïdes !
Allez, j’arrête là le teaser, cette courbe mystère s’appelle une clothoïde, ou spirale d’Euler, ou encore juste spirale pour les intimes.
Il s’agit d’une courbe qui répond à une formulation mathématique bien précise. Elle définit une progression linéaire de son rayon de courbure tout au long de son trajet.
Par définition, le rayon de courbure, c’est :
- le rayon du cercle, dans notre cas des rails de second type,
- l’infini pour les rails droits (on peut assimiler qui s’agirait des mêmes rails mais au rayon qui serait infini).
Si l’on suit la séquence suivante (appelé “S-C-S” pour Spirale-Courbe-Spirale) :
- rail-droit, R = +∞,
- rail-spirale, R : +∞ → cm,
- rail-courbe, R = 60 cm,
- rail-spirale, R : 60 cm → +∞,
- rail-droit, R = +∞,
le voyage du train devient beaucoup plus doux, et il n’y a plus de déraillements !
Pour mieux comprendre ce que cela change, prenons un autre exemple de construction ferroviaire :
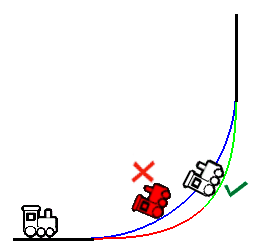
Ici, le trajet bleu est uniquement composé d’arcs de cercle de rayon 60 cm, alors que le trajet rouge et vert est composé de 2 spirales.
Si l’on représente maintenant la courbure (1/R) le long du chemin, on obtient ceci :
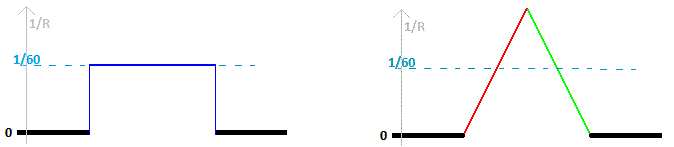
On observe que le deuxième trajet est plus long que l’autre, par contre le train ne rencontre plus de discontinuité de courbure. Ce type de courbe est utilisé dans de nombreux ouvrages de génie civil : les routes, les ponts, les réseaux ferroviaires, la mécanique.
Vous y penserez peut-être la prochaine fois que vous prendrez une sortie d’autoroute tout en douceur, même à 100 km/h.
Pourquoi une clothoïde s’appelle-t-elle aussi une spirale ?
Si on rentre un peu plus dans la mathématique de la courbe, et que l’on dessine la courbe sur un trajet infini on obtient ce graphique :
On obtient donc 2 spirales symétriques.
Pour la suite de cet article, nous utiliserons les symboles suivants :
| R | Rayon de courbure en un point donné du trajet. On posera que R = +∞ au début du trajet. |
|---|---|
| φ | Angle entre la tangente au trajet en un point donné et l’axe des abscisses. φ = 0 au début. |
| L | Distance parcourue le long de la courbe en un point donné. L = 0 au début. |
| A | Paramètre constant qui définit comment évolue le rayon de courbure le long du trajet, par définition : 1/R = L x 1/A2, c’est a dire A2 = RL |
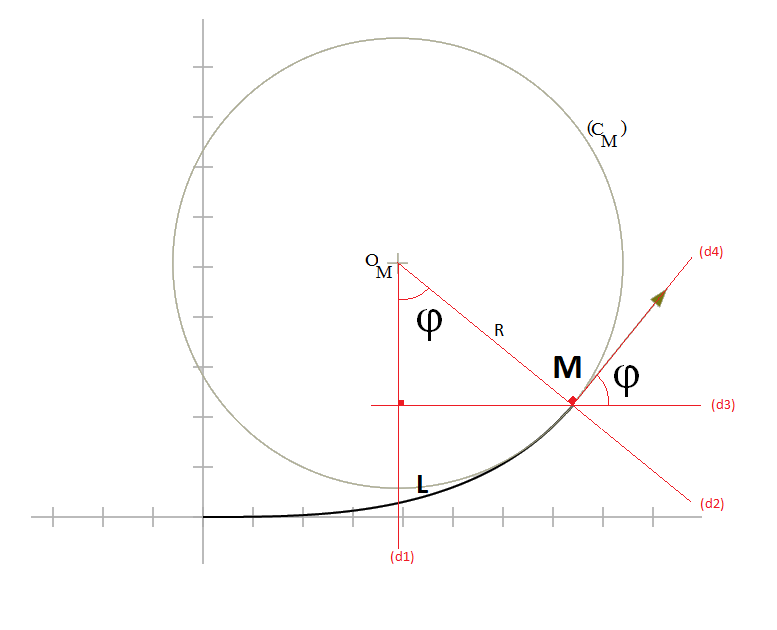
Notez également que sur ce dessin que les deux angles notes φ sont bien les mêmes :
- φ l’angle interne entre (d1) et (d2).
- (d3) est perpendiculaire à (d1) par construction.
- (d4) est perpendiculaire à (d2), puisqu’il s’agit de la tangente au cercle CM au point M.
- Donc l’angle entre (d3) et (d4) vaut φ également.
Dessine-moi une clothoïde !
Nous allons essayer maintenant de dessiner notre propre spirale.
Si on imagine le trajet du point M(x,y) le long d’un trajet allant :
- de l’abscisse curviligne L1 (=0),
- à l’abscisse curviligne L2 (=L la longueur du trajet),
on obtient :
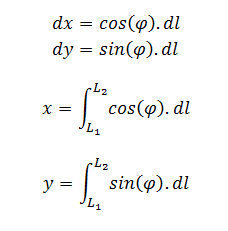
Notez que φ dépend de l, en effet :
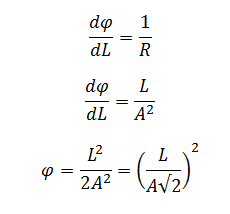
Donc en posant :
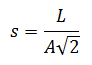
On obtient plutôt :
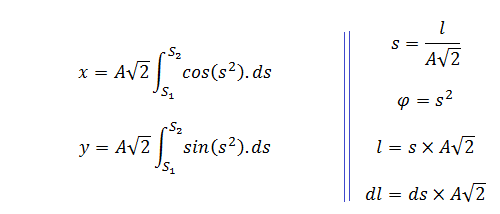
Ce qui amène le code JavaScript suivant :
function drawSpiral(A, L1, L2)
{
var a = A*Math.sqrt(2);
var S1 = L1/a;
var S2 = L2/a;
var s=S1;
var ds = Math.abs(S2-S1)/10000;
var M = new Point(0,0);
while (s
Résultat
- Lenght :
- StartRadius :
- isCCW:
- isEntry:
- ClothoideConstant:
